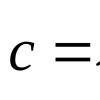С n неизвестными это система вида:

где a ij и b i (i=1,…,m; b=1,…,n) - некоторые известные числа, а x 1 ,…,x n - неизвестные числа. В обозначении коэффициентов a ij индекс i определяет номер уравнения, а второй j - номер неизвестного, у которого расположен этот коэффициент.

Однородная система - когда все свободные члены системы равны нулю (b 1 = b 2 = … = b m = 0 ), обратная ситуация — неоднородная система .

Квадратная система - когда число m уравнений равняется числу n неизвестных.

Решение системы — совокупность n чисел c 1 , c 2 , …, c n , таких, что подстановка всех c i вместо x i в систему превращает все её уравнения в тождества .

Совместная система - когда у системы есть хоть бы 1-но решение, и несовместная система , когда у системы нет решений.

У совместной системы такого вида (как приведен выше, пусть она будет (1)) может быть одно либо больше решений.

Решения c 1 (1) , c 2 (1) , …, c n (1) и c 1 (2) , c 2 (2) , …, c n (2) совместной системы типа (1) будут различными , когда не выполняется даже 1-но из равенств:

c 1 (1) = c 1 (2) , c 2 (1) = c 2 (2) , …, c n (1) = c n (2) .

Совместная система типа (1) будет определённой , когда у нее есть только одно решение; когда у системы есть хотя бы 2 разных решений, она становится недоопределённой . Когда уравнений больше, чем неизвестных, система является переопределённой .

Коэффициенты при неизвестных записываются как матрица:

Она называется матрицей системы .

Числа, которые стоят в правых частях уравнений, b 1 ,…,b m являются свободными членами .

Совокупность n чисел c 1 ,…,c n является решением этой системы, когда все уравнения системы обращаются в равенство после подставки в них чисел c 1 ,…,c n вместо соответствующих неизвестных x 1 ,…,x n .

При решении системы линейных уравнений могут возникнуть 3 варианта:

1. У системы есть только одно решение.

2. У системы есть нескончаемое число решений. Например , . Решением этой системы будут все пары чисел, которые отличаются знаком.

3. У системы нет решений. Например , , если бы решение существовало, то x 1 + x 2 равнялось бы в одно время 0 и 1.

Методы решения систем линейных уравнений.

Прямые методы дают алгоритм, по которому находится точное решение СЛАУ (систем линейных алгебраических уравнений). И если бы точность была абсолютной, они бы нашли его. Реальная электро-вычислительная машина, конечно, работает с погрешностью, поэтому решение будет приблизительным.

В общем случае линейное уравнение имеет вид:

Уравнение имеет решение: если хотя бы один из коэффициентов при неизвестных отличен от нуля. В этом случае любой -мерный вектор называется решением уравнения, если при подстановке его координат уравнение обращается в тождество.

Общая характеристика разрешенной системы уравнений

Пример 20.1

Дать характеристику системе уравнений .

Решение :

1. Входит ли в состав противоречивое уравнение? (Если коэффициенты, в этом случае уравнение имеет вид: и называется противоречивым .)

• Если система содержит противоречивое, то такая система несовместна и не имеет решения

2. Найти все разрешенные переменные . (Неизвестная называется разрешенной для системы уравнений, если она входит в одно из уравнений системы с коэффициентом +1, а в остальные уравнения не входит (т.е. входит с коэффициентом, равным нулю).

3. Является ли система уравнений разрешенной? (Система уравнений называется разрешенной , если каждое уравнение системы содержит разрешенную неизвестную, среди которых нет совпадающих)

Разрешенные неизвестные, взятые по одному из каждого уравнения системы, образуют полный набор разрешенных неизвестных системы. (в нашем примере это )

Разрешенные неизвестные, входящие в полный набор, называют также базисными (), а не входящие в набор — свободными ().

В общем случае разрешенная система уравнений имеет вид:

На данном этапе главное понять что такое разрешенная неизвестная (входящая в базис и свободная).

Общее Частное Базисное решения

Общим решением разрешенной системы уравнений называется совокупность выражений разрешенных неизвестных через свободные члены и свободные неизвестные:

Частным решением называется решение, получающиеся из общего при конкретных значениях свободных переменных и неизвестных.

Базисным решением называется частное решение, получающееся из общего при нулевых значениях свободных переменных.

• Базисное решение (вектор) называется вырожденным , если число его координат, отличных от нуля, меньше числа разрешенных неизвестных.
• Базисное решение называется невырожденным , если число его координат, отличных от нуля, равно числу разрешенных неизвестных системы, входящих в полный набор.

Теорема (1)

Разрешенная система уравнений всегда совместна (потому что она имеет хотя бы одно решение); причем если система не имеет свободных неизвестных, (то есть в системе уравнений все разрешенные входят в базис) то она определена (имеет единственное решение); если же имеется хотя бы одна свободная переменная, то система не определена (имеет бесконечное множество решений).

Пример 1. Найти общее, базисное и какое-либо частное решение системы уравнений:

Решение :

1. Проверяем является ли система разрешенной?

• Система является разрешенной (т.к. каждое из уравнений содержит в себе разрешенную неизвестную)

2. Включаем в набор разрешенные неизвестные — по одному из каждого уравнения .

3. Записываем общее решение в зависимости от того какие разрешенные неизвестные мы включили в набор .

4. Находим частное решение . Для этого приравниваем свободные переменные, которые мы не включили в набор приравнять к произвольным числам.

Ответ: частное решение (один из вариантов)

5. Находим базисное решение . Для этого приравниваем свободные переменные, которые мы не включили в набор к нулю.

Элементарные преобразования линейных уравнений

Системы линейных уравнений приводятся к равносильным разрешенным системам с помощью элементарных преобразований.

Теорема (2)

Если какое-либо уравнение системы умножить на некоторое отличное от нуля число , а остальные уравнения оставить без изменения, то . (то есть если умножить левую и правую часть уравнения на одно и то же число то получится уравнение, равносильное данному)

Теорема (3)

Если к какому-либо уравнению системы прибавить другое , а все остальные уравнения оставить без изменения, то получится система, равносильная данной . (то есть если сложить два уравнения (сложив их левые и правые части) то получится уравнение равносильное данным)

Следствие из Теорем (2 и 3)

Если к какому-либо уравнению прибавить другое, умноженное на некоторое число , а все остальные уравнения оставить без изменения, то получится система, равносильная данной .

Формулы пересчета коэффициентов системы

Если у нас есть система уравнений и мы хотим преобразовать ее в разрешенную систему уравнений в этом нам поможет метод Жордана-Гаусса.

Преобразование Жордана с разрешающим элементом позволяет получить для системы уравнений разрешенную неизвестную в уравнении с номером . (пример 2).

Преобразование Жордана состоит из элементарных преобразований двух типов:

Допустим мы хотим сделать неизвестную в нижнем уравнении разрешенной неизвестной. Для этого мы должны разделить на , так чтобы сумма .

Пример 2 Пересчитаем коэффициенты системы

При делении уравнения с номером на , его коэффициенты пересчитываются по формулам:

Чтобы исключить из уравнения с номером , нужно уравнение с номером умножить на и прибавить к этому уравнению.

Теорема (4) О сокращении числа уравнений системы.

Если система уравнений содержит тривиальное уравнение, то его можно исключить из системы, при этом получится система равносильная исходной.

Теорема (5) О несовместимости системы уравнений.

Если система уравнений содержит противоречивое уравнение, то она несовместна.

Алгоритм метода Жордана-Гаусса

Алгоритм решения систем уравнений методом Жордана-Гаусса состоит из ряда однотипных шагов, на каждом из которых производятся действия в следующем порядке:

1. Проверяется, не является ли система несовместной. Если система содержит противоречивое уравнение, то она несовместна.
2. Проверяется возможность сокращения числа уравнений. Если в системе содержится тривиальное уравнение, его вычеркивают.
3. Если система уравнений является разрешенной, то записывают общее решение системы и если необходимо — частные решения.
4. Если система не является разрешенной, то в уравнении, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом.
5. Далее заново переходят к пункту 1

Пример 3 Решить систему уравнений методом Жордана-Гаусса.

Найти : два общих и два соответствующих базисных решения

Решение :

Вычисления приведены в нижеследующей таблице:

Справа от таблицы изображены действия над уравнениями. Стрелками показано к какому уравнению прибавляется уравнение с разрешающим элементом, умноженное на подходящий множитель.

В первых трех строках таблицы помещены коэффициенты при неизвестных и правые части исходной системы. Результаты первого преобразования Жордана с разрешающим элементом равным единице приведены в строках 4, 5, 6. Результаты второго преобразования Жордана с разрешающим элементом равным (-1) приведены в строках 7, 8, 9. Так как третье уравнение является тривиальным, то его можно не учитывать.

Решение систем линейных алгебраических уравненийявляется одной из основных задач линейной алгебры. Эта задача имеет важное прикладное значение при решении научных и технических проблем, кроме того является вспомогательной при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований.

Системой линейных алгебраических уравнений называют систему уравнений вида: (1)

где – неизвестные; – свободные члены.

Решением системы уравнений (1) называют всякую совокупность чисел которая будучи поставлена в систему (1) на место неизвестных обращает все уравнения системы в верные числовые равенства.

Систему уравнений называют совместной , если она имеет хотя бы одно решение, и несовместной , если не имеет решений.

Совместную систему уравнений называют определенной , если она имеет одно единственное решение, и неопределенной , если она имеет, по крайней мере, два различных решения.

Две системы уравнений называют равносильными или эквивалентными , если они имеют одно и то же множество решений.

Систему (1) называют однородной , если свободные члены равны нулю:

Однородная система всегда является совместной - она имеет решение (возможно, не единственное).

Если в системе (1) , то имеем систему n линейных уравнений с n неизвестными: где – неизвестные; – коэффициенты при неизвестных, – свободные члены.

Линейная система может иметь единственное решение, бесконечно много решений или не иметь ни одного решения.

Рассмотрим систему двух линейных уравнений с двумя неизвестными

Если то система имеет единственное решение;

если то система не имеет решений;

если то система имеет бесконечное множество решений.

Пример. Система имеет единственное решение пару чисел

Система имеет бесконечное множество решений. Например, решениями данной системы являются пары чисел и т.д.

Система не имеет решений, так как разность двух чисел не может принимать двух различных значений.

Определение. Определителем второго порядка называют выражение вида:

Обозначают определитель символом D.

Числа а 11, …, а 22 называют элементами определителя.

Диагональ, образованную элементами а 11 ; а 22 называют главной, диагональ, образованную элементами а 12 ; а 21 − побочной.

Таким образом, определитель второго порядка равен разности произведений элементов главной и побочной диагоналей.

Заметим, что в ответе получается число.

Пример. Вычислим определители:

Рассмотрим систему двух линейных уравнений с двумя неизвестными: где х 1, х 2 – неизвестные; а 11 , …, а 22 – коэффициенты при неизвестных, b 1 , b 2 – свободные члены.

Если система двух уравнений с двумя неизвестными имеет единственное решение, то его можно найти с помощью определителей второго порядка.

Определение. Определитель, составленный из коэффициентов при неизвестных, называют определителем системы: D= .

В столбцах определителя D стоят коэффициенты соответственно при х 1 и при , х 2 . Введем два дополнительных определителя, которые получаются из определителя системы заменой одного из столбцов столбцом свободных членов: D 1 = D 2 = .

Теорема 14 (Крамера, для случая n=2). Если определитель D системы отличен от нуля (D¹0), то система имеет единственное решение, которое находят по формулам:

Данные формулы называют формулами Крамера.

Пример. Решим систему по правилу Крамера:

Решение. Найдем числа

Ответ.

Определение. Определителем третьего порядка называют выражение вида:

Элементы а 11; а 22 ; а 33 – образуют главную диагональ.

Числа а 13; а 22 ; а 31 – образуют побочную диагональ.

В запись с плюсом входят: произведение элементов на главной диагонали, остальные два слагаемых являются произведением элементов, расположенных в вершинах треугольников с основаниями, параллельными главной диагонали. Слагаемые с минусом образуют по той же схеме относительно побочной диагонали.

Пример. Вычислим определители:

Рассмотрим систему трех линейных уравнений с тремя неизвестными: где – неизвестные; – коэффициенты при неизвестных, – свободные члены.

В случае единственного решения систему 3-х линейных уравнений с тремя неизвестными можно решить с помощью определителей 3-го порядка.

Определитель системы D имеет вид:

Введем три дополнительных определителя:

Теорема 15 (Крамера, для случая n=3). Если определитель D системы отличен от нуля, то система имеет единственное решение, которое находят по формулам Крамера:

Пример. Решим систему по правилу Крамера.

Решение. Найдем числа

Воспользуемся формулами Крамера и найдем решение исходной системы:

Ответ.

Заметим, что теорема Крамера применима, когда число уравнений равно числу неизвестных и когда определитель системы D отличен от нуля.

Если определитель системы равен нулю, то в этом случае система может либо не иметь решений, либо иметь бесчисленное множество решений. Эти случаи исследуются особо.

Отметим только один случай. Если определитель системы равен нулю (D=0), а хотя бы один из дополнительных определителей отличен от нуля, то система решений не имеет, то есть является несовместной.

Теорему Крамера можно обобщать для системы n линейных уравнений с n неизвестными: где – неизвестные; – коэффициенты при неизвестных, – свободные члены.

Если определитель системы линейных уравнений с неизвестными то единственное решение системы находят по формулам Крамера:

Дополнительный определитель получают из определителя D, если в нем столбец коэффициентов при неизвестном x i заменить столбцом свободных членов.

Заметим, что определители D, D 1 , … , D n имеют порядок n .

Метод Гаусса решения систем линейных уравнений

Одним из наиболее распространенных методов решения систем линейных алгебраических уравнений является метод последовательного исключения неизвестных −метод Гаусса . Данный метод представляет собой обобщение метода подстановки и состоит в последовательном исключении неизвестных до тех пор, пока не останется одно уравнение с одним неизвестным.

Метод основан на некоторых преобразованиях системы линейных уравнений, в результате которых получается система, равносильная исходной системе. Алгоритм метода состоит из двух этапов.

Первый этап называют прямым ходом метода Гаусса. Он заключается в последовательном исключении неизвестных из уравнений. Для этого на первом шаге делят первое уравнение системы на ( в противном случае осуществляют перестановку уравнений системы). Обозначают коэффициенты полученного приведенного уравнения, домножают его на коэффициент и вычитают из второго уравнения системы, исключая, тем самым, из второго уравнения (обнуляя коэффициент ).

Аналогично поступают с остальными уравнениями и получают новую систему, во всех уравнениях которой, начиная со второго коэффициенты при , содержатся только нули. Очевидно, что полученная при этом новая система, будет равносильна исходной системе.

Если новые коэффициенты, при , не все равны нулю, можнотаким же образом исключить из третьего и последующих уравнений. Продолжая эту операцию для следующих неизвестных, приводят систему к так называемому треугольному виду:

Здесь символами и обозначены изменившиеся в результате преобразований числовые коэффициенты и свободные члены.

Из последнего уравнения системы единственным образом определяют , а затем последовательной подстановкой – остальные неизвестные.

Замечание. Иногда, в результате преобразований, в каком-либо из уравнений все коэффициенты и правая часть обращаются в ноль, то есть уравнение превращается в тождество 0=0. Исключив такое уравнение из системы, уменьшают число уравнений по сравнению с числом неизвестных. Такая система не может иметь единственного решения.

Если же в процессе применения метода Гаусса какое-нибудь уравнение превратится в равенство вида 0=1 (коэффициенты при неизвестных обратились в 0, а правая часть приняла ненулевое значение), то исходная система не имеет решения, так как подобное равенство является неверным при любых значениях неизвестных.

Рассмотрим систему трех линейных уравнений с тремя неизвестными:

где – неизвестные; – коэффициенты при неизвестных, – свободные члены. , подставляя найденное

Решение. Применив к этой системе метод Гаусса, получим

Откуда Последнее равенство является неверным при любых значениях неизвестных, следовательно, система не имеет решения.

Ответ. Система не имеет решений.

Заметим, что рассмотренный ранее метод Крамера можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений.

Системой m линейных уравнений с n неизвестными называется система вида

где a ij и b i (i =1,…,m ; b =1,…,n ) – некоторые известные числа, а x 1 ,…,x n – неизвестные. В обозначении коэффициентов a ij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы .

Числа, стоящие в правых частях уравнений, b 1 ,…,b m называются свободными членами.

Совокупность n чисел c 1 ,…,c n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c 1 ,…,c n вместо соответствующих неизвестных x 1 ,…,x n .

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной . В противном случае, т.е. если система не имеет решений, то она называется несовместной .

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

Найдем произведение

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

или короче A ∙X=B .

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением .

Пусть определитель матрицы отличен от нуля |A | ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A : . Поскольку A -1 A = E и E ∙X = X , то получаем решение матричного уравнения в виде X = A -1 B .

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных . Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B .

Примеры. Решить системы уравнений.

ПРАВИЛО КРАМЕРА

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы .

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство . Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A 11 элемента a 11 , 2-ое уравнение – на A 21 и 3-е – на A 31 :

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

МЕТОД ГАУССА

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x 1 . Для этого второе уравнение разделим на а 21 и умножим на –а 11 , а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а 31 и умножим на –а 11 , а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x 2 . Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x 3 , затем из 2-го уравнения x 2 и, наконец, из 1-го – x 1 .

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

1. перестановка строк или столбцов;
2. умножение строки на число, отличное от нуля;
3. прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

Таким образом, система имеет бесконечное множество решений.

Запишите систему линейных алгебраических уравнений в общем виде

Что называется решением СЛАУ?

Решением системы уравнений называется набор из n чисел,

При подстановке которой в систему каждое уравнение обращается в тождество.

Какая система называется совместной (несовместной)?

Система уравнений называется совместной, если она имеет хотя бы одно решение.

Система называется несовместной, если она не имеет решений.

Какая система называется определенной (неопределенной)?

Совместная система называется определенной, если она имеет единственное решение.

Совместная система называется неопределенной, если она имеет больше одного решения.

Матричная форма записи системы уравнений

Ранг системы векторов

Ранг системы векторов называется максимальное число линейно независимых векторов.

Ранг матрицы и способы его нахождения

Ранг матрицы - наивысший из порядков миноров этой матрицы, определитель которых отличен от нуля.

Первый метод –- метод окантовки - заключается в следующем:

Если все миноры 1-го порядка, т.е. элементы матрицы равны нулю, то r=0 .

Если хоть один из миноров 1-го порядка не равен нулю, а все миноры 2-го порядка равны нулю то r=1.

Если минор 2-го порядка отличен от нуля то исследуем миноры 3-го порядка. Таким образом находят минор k-го порядка и проверяют, не равны ли нулю миноры k+1-го порядка.

Если все миноры k+1-го порядка равны нулю, то ранг матрицы равен числу k. Такие миноры k+1-го порядка, как правило, находят путем "окантовки" минора k-го порядка.

Второй метод определения ранга матрицы заключается в применении элементарных преобразований матрицы при возведении ее к диагональному виду. Ранг такой матрицы равно числу отличных от нуля диагональных элементов.

Общее решение неоднородной системы линейных уравнений, его свойства.

Свойство 1. Сумма любого решения системы линейных уравнений и любого решения соответствующей однородной системы является решением системы линейных уравнений.

Свойство 2. Разность любых двух решений неоднородной системы линейных уравнений является решением соответствующей однородной системы.

Метод Гаусса решения СЛАУ

Последовательность:

1)составляется расширенная матрица системы уравнения

2)с помощью элементарных преобразований матрица приводится к ступенчатому виду

3)определяется ранг расширенной матрицы системы и ранг матрицы системы и устанавливается пакт совместимости или несовместимости системы

4)в случае совместимости записывается эквивалентная система уравнения

5)находится решение системы. Главные переменные выражаются через свободные

Теорема Кронекера-Капелли

Теоре́ма Кро́некера - Капе́лли - критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Для того чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу её основной матрицы.

Когда система не имеет решения, когда имеет единственное решение, имеет множество решений?

Если число уравнений системы равно числу неизвестных переменных и определитель ее основной матрицы не равен нулю,значит Такие системы уравнений имеют единственное решение, причем в случае однородной системы все неизвестные переменные равны нулю.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.