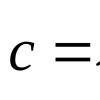Пусть с испытанием связаны n случайных величин 1 , 2 ,….,ξ n . Укажем кратко, как введенные в этой главе понятия переносятся на этот случай.
1. Совместной функцией распределения случайных величин 1 , 2 ,….,ξ n называется функция
Совместной плотностью вероятности случайных величин 1 , 2 ,….,ξ n называется функция
Имеет место равенство
2. Обозначим а i , σ j математическое ожидание и СКО случайной величины ξ i , к ij – ковариацию случайных величин ξ i , ξ j:
называется дисперсионной матрицей случайных величин 1 , 2 ,….,ξ n . Отметим следующие свойства матрицы D.
1 0 . Элементы главной диагонали матрицы D – дисперсии случайных величин 1 , 2 ,….,ξ n:
2 0 . Матрица D симметрическая: k ij =k ji .
3 0 . Собственные числа матрицы D неотрицательны.
Свойства 1 0 , 2 0 очевидны. Предлагаем читателю проверить свойство 3 0 для частного случая n=2. В этом случае матрица D имеет вид
(28)
где r – коэффициент корреляции случайных величин 1 , 2 .
3. В §3 этой главы было введено понятие совместного нормального распределения случайных величин 1 , 2 – см.формулу (25). Это понятие обобщается следующим образом. Говорят, что случайные величины 1 , 2 ,….,ξ n имеют совместное нормальное распределение, если совместная плотность вероятности дается формулой
где
-
определитель дисперсионной матрицыD,
с ij – элементы матрицы C=D -1 .
Нетрудно проверить, что в частном случае n=2 это определение совпадает с определением (25); для этого нужно воспользоваться формулой (28) для матрицы D и формулой обращения матрицы второго порядка с отличным от нуля определителем:
(предлагаем читателю выполнить проверку самостоятельно).
Справедливы утверждения: если 1 , 2 ,….,ξ n имеют совместное нормальное распределение, то каждая из них отдельно также нормальна; если каждая ξ i нормальна и при этом 1 , 2 ,….,ξ n независимы, то их совместное распределение также нормально, и имеет место формула
где f i (x) – плотность вероятности ξ i . В общей ситуации из нормальности каждой отдельно ξ i не вытекает нормальность совместного распределения.
Понятие совместного нормального распределения играет важную роль в приложениях теории вероятностей.
Глава 5. Закон больших чисел. Предельные теоремы
Под законом больших чисел понимают закономерности вмассовых случайных явлениях, когда взаимодействие большого числа случайных факторов приводит к неслучайному результату. Пример закономерности такого типа приведен во введении: доля наступления случайного события в длинной серии независимых одинаковых испытаний практически неслучайна. Другой замечательный пример: оказывается, в ряде случаев закон распределения суммы большого числа случайных слагаемых не зависит от законов распределения слагаемых и может быть предсказан! Назначение предельных теорем теории вероятностей: дать строгие формулировки и обоснования различных форм закона больших чисел. В этой главе мы кратко рассмотрим результаты такого типа.
§1. Закон больших чисел в форме Чебышева
На практике хорошо известна следующая закономерность, которую можно сформулировать так: среднее арифметическое большого числа независимых однотипных случайных факторов практически неслучайно. Например, среднее арифметическое большого числа измерений одной и той же величины практически не отличается от истинного значения этой величины; средняя кинетическая энергия большого числа хаотически движущихся молекул практически неслучайна и характеризует температуру тела.
Методы теории вероятностей позволяют дать строгую математическую формулировку этого закона.
Пусть имеется бесконечная последовательность случайных величин
1 , 2 , … , n , … (29)
Будем кратко называть случайные величины (29) однотипными, если они имеют одно и тоже математическое ожиданиеа и одну и туже дисперсиюD .
Теорема. Пусть случайные величины (29) однотипны и независимы, тогда имеет место соотношение
приn
,
(30)
где а =М [ k ],k = 1, 2, …, – любое как угодно малое положительное число.
Это означает: при достаточно большом n с практической достоверностью (с вероятностью100%) выполняется равенство
.
Эта теорема впервые была доказана русским математиком П.Л. Чебышевым. Доказательство теоремы основано на трех леммах.
Лемма 1. Пусть случайная величина≥ 0. Тогда справедливо неравенство
Р
(≥)
≤
,
(31)
где – любое положительное число.
Доказательство проведем для непрерывной случайной величины. Плотность вероятности случайной величиныf (х ) = 0 прих < 0, так как≥ 0.
По определению математического ожидания имеем:
≥
≥
(≥),
откуда следует неравенство (31).
Лемма 2. Пусть– случайная величина с числовыми характеристиками (а ,D ), тогда справедливо неравенство:
Р
(|–a
| <
) ≥ 1 –
.
Доказательство. Имеем
Р
(|–a
| ≥
) =P
((–a
) 2 ≥
2) ≤
.
Здесь использовано неравенство (31) при = ( – a ) 2 , = 2 .
Из полученного неравенства следует
Р
(|–a
| <
) = 1 –Р
(|–a
| ≥
) ≥ 1 –
.
Лемма 3. Пусть 1 , 2 , …, n - независимые однотипные случайные величины с числовыми характеристиками (а ,D). Тогда при любом>0 справедливо неравенство
≥ 1 –
.
(32)
где – любое положительное число, a = M [ i ],D = D [ i ],i = 1, 2, …,n ..
Неравенство (32) называется неравенством Чебышева .
Доказательство. Обозначим
.
Из свойств математического ожидания и дисперсии для независимых случайных величин следует:
Таким образом,
случайная величина
имеет числовые характеристики
;
применяя к ней лемму 2, получим требуемое
неравенство (32).
Доказательство теоремы Чебышева.
В силу неравенства Чебышева (32) имеем при любом n двойное неравенство
1 ≥
≥ 1 –
.
Переходя к пределу при n и учитывая теорему сравнения из теории пределов, получим требуемое соотношение (30).
Замечание. Введем удобный термин. Пусть имеется последовательность случайных величин
1 , 2 , …, n , … . (33)
Говорят, что последовательность (33) сходится по вероятности к неслучайной величинеа и пишут
приn
,
если для любого > 0 выполняется соотношение
Р (| n –a | < )1 приn .
Очевидно, теорема Чебышева может быть сформулирована так: среднее арифметическое независимых однотипных случайных величин при неограниченном увеличении числа слагаемых сходится по вероятности к их общему математическому ожиданию.
Пример. Сколько надо провести независимых равноточных измерений данной величины, чтобы с вероятностью не менее 0,95 гарантировать отклонение среднего арифметического этих измерений от истинного значения величины не более, чем на 1 (по абсолютной величине), если СКО каждого измерения не превосходит 5?
Решение. Пусть i – результатi -го измерения (i = 1,2,…,n ),a – истинное значение измеряемой величины, то естьM [ i ] =a при любомi ; с учетом равноточности измерений i имеют одинаковую дисперсиюD≤ 25. В силу независимости измерений i – независимые случайные величины.
Необходимо найти n , при котором
≥ 0,95.
В соответствии с неравенством Чебышева (32) данное неравенство будет выполняться, если
1 –
≥ 1–
≥
0,95, откуда легко найти
n ≥500 измерений.
Совместное распределение нескольких случайных величин
Для изучения системы случайных величин нужно знать закон совместного распределения их вероятностей. Рассмотрим систему 2-х случайных величин x и y , ᴛ.ᴇ. двумерную случайную величину. Систему двух случайных величин рассматриваем как систему двух одномерных величин. Каждую из величин x и y называют компонентой двумерной случайной величины. Двумерную случайную величину называют дискретной если ее компоненты дискретны.
(x i ; y j) – возможные
Случайная величина представляет систему двух случайных величин ее декартовых координат. Задание закона ее совместного распределения величин x и y означает задание вероятности попадания случайной точки величины x, y в точку x i ; y j . Вероятность Р(x=x i ; y=y j )=P i,j , i =1……n; j =1……..m . Эти вероятности бывают любыми неотрицательными числами, сумма которых равна 1. Т.к. события x=x i ; y=y j образуют полную группу. Т.е. закон распределения задан в виде таблицы с двумя входами. 1 столбец содержит все возможные значения x , а первая строка все возможные значения компоненты y , каждую вероятность P i,j можно рассматривать как совмещение случайных событий x=x i ; y=y j .
| y 1 | y 2 ………. | y m | |||
| x 1 | P 11 | P 12 | P 1m | |||
| x 2 | P 21 | P 22 | P 2n | |||
| x n | P n1 | P n2 | P nm |
Две дискретные величины x, y называются независимыми, в случае если для всех их возможных значений x i ; y j имеет место равенство
P i,j =Р(Х=x i)×P(Y=y j)
Это определение распределения и наибольшее число дискретных случайных величин.
Пример: В первом ящике 6 шаров, во вором также 6 шаров
I 1 шар с номером 1
2 шара с номером 2 Х - № из I ящика
3 шара с номером 3
II 2 шара с номером 1
3 шара с номером 2 Х - № из II ящика
1 шар с номером 3
Из каждого ящика взяли по шару, составить таблицу закона распределения системы случайных величин. Найти законы распределения составляющих.
| x | |||
| P |
| y | |||
| P |
| y 1 | y 2 | y 3 | ||
| x 1 x 2 x 3 | ||||
Пусть (х, у) – двумерная непрерывная случайная величина. Двумерную случайную величину (х, у) – называют непрерывной, в случае если ее компоненты непрерывны. Кроме того величины х, у обладают непрерывной плотностью распределения.
P(x
Как дифференцируемая функция
Функция удовлетворяет 2-м основным свойствам f(x,y)³ 0 и двойной интеграл
Вероятность попадания случайной точки в любую область D на плоскости х, у , должна быть представлена в виде двойного интеграла:
Функция распределения должна быть выражена, как:
F(x;y)=
График плотности распределения называют поверхностью распределения вероятности.
Пример: Найти функцию распределения двумерной случайной величины с плотностью распределения:
f(x;y)=e -x-y (x³0,y³0)
P(0
Распределение компонент непрерывной случайной величины (х; у).
 |
т.к. попадание абсциссы в интервале равносильно попаданию точки в вертикальную область D , то вероятности этих событий равны.
Данный интеграл можно записать и таким образом
Сравним с другим равенством. Согласно определению плотности распределения следует, что искомая плотность равна
,
Аналогично площадь распределения величины у будет равна
Эти понятия обобщаются для систем более 2-х величин.
Определение: Непрерывные случайные величины х и у называются независимыми, в случае если плотность совместного распределения равна произведению плотности этих величин
Условие независимости.
Совместное распределение нескольких случайных величин - понятие и виды. Классификация и особенности категории "Совместное распределение нескольких случайных величин" 2017, 2018.
Пусть пространство элементарных исходов W случайного эксперимента таково, что каждому исходу w i j ставиться в соответствие значение случайной величины X, равное x i и значение случайной величины Y, равное y j .
1. Представим себе упаковку деталей, характеризующихся 2-я габаритными размерами. Случайный эксперимент заключается в случайном выборе одной детали. Эта деталь имеет длину, которую будем обозначать X и толщину-Y
2. Если результат эксперимента – выбор студента для представления к повышенной стипендии. Тогда Х и Y – средние баллы за последние две сессии
В этом случае мы можем говорить о совместном распределении случайных величин X и Y или о “двумерной” случайной величине.
Если X и Y дискретны и принимают конечное число значений (X – n значений, а Y – m значений), то закон совместного распределения случайных величин X и Y можно задать, если каждой паре чисел x i , y j (где x i принадлежит множеству значений X, а y j -множеству значений Y) поставить в соответствие вероятность p ij , равную вероятности события, объединяющего все исходы w ij (и состоящего лишь из этих исходов), которые приводят к значениям X = x i ; Y = y j .
Такой закон распределения можно задать в виде таблицы:
а первая и последняя строки дают ряд распределения случайной величины Y. Таблица является законом распределения двумерной дискретной случайной величины, если сумма вероятностей в последней строке или в последнем столбце (и соответственно, сумма вероятностей внутри таблицы) = 1.
Пользуясь этой таблицей, по аналогии с одномерным случаем, можно определить совместную функцию распределения. Для этого необходимо просуммировать р ij по всем i, j для которых x i < x, y j < y
Рассмотрим пример («ТВ» МГТУ им.Баумана)
В соответствии со схемой Бернулли с вероятностью успеха p, и вероятностью неудачи q =1-p проводятся 2 испытания.
Рассмотрим распределение двумерного вектора (Х 1 , Х 2), каждая из которых может принимать 2 значения: 0 или 1 (число успехов в соответствующем опыте) . Число успехов в обоих испытаниях равно 0, когда произойдут 2 неудачи, а это в силу независимости равно qq. Поэтому
и на пересечении «0» столбцов пишем q 2 .
Совместная функция распределения F (x 1 , x 2 ) задает поверхность в трехмерном пространстве.
Определение . Условным законом распределения (X |Y=y j)(j сохраняет одно и то же значение при всех значениях Х) называют совокупность условных вероятноястей р(x 1 |y j), р(x 2 |y j),… р(x n |y j), а условные вероятности вычисляются по формулам:
р(X=x i |Y=y j) = р(X=x i ,Y=y j) / р(Y=y j)
Пример. Задана дискретная двумерная величина
| X | |||
| P | 0,2 | 0,32 | 0,48 |
р(X=x 1 |Y=y 1) = р(X=x 1 ,Y=y 1) / р(Y=y 1)= 0,15/0,8 = 3/16
р(X=x 2 |Y=y 1) = р(X=x 2 ,Y=y 1) / р(Y=y 1)=0,3/0,8 = 3/8
р(X=x 3 |Y=y 1) = р(X=x 3 ,Y=y 1) / р(Y=y 1) = 0,35/0,8 = 7/16
| X | |||
| р(X |Y=y 1) | 3/16 | 3/8 | 7/16 |
Проверка: сумма вероятностей равна 1.
Замечание . Таким образом, можно проверить и независимость случайных величин. Аналогично случаю независимости событий, независимость случайных величин может быть определена через условные вероятности. Остается только сравнить условный и безусловный законы распределения.
Пример.
Рассмотрим коробку, в которой лежат две карточки с цифрой 1 и три карточки с цифрой 2. Одна за другой вынимаются две карточки. X – номер на первой карточке. Y – на второй. Найти совместный закон распределения (X,Y)
Используем формулу произведения вероятностей P((X,Y)=(1,1)) = P(X=1)P(Y=1|X=1)=2/5× ¼ = 1/10
| (X,Y) | (1,1) | (1,2) | (2,1) | (2,2) |
| P | 1/10 | 3/10 | 3/10 | 3/10 |
Сумма вероятностей = 1.
Воспользуемся изложенным выше общим методом для решения одной задачи, а именно для нахождения закона распределения суммы двух случайных величин. Имеется система двух случайных величин (X,Y) с плотностью распределения f(x,у).
Рассмотрим сумму случайных величин X и Y: и найдем закон распределения величины Z. Для этого построим на плоскости хОу линию, уравнение которой 
(рис. 6.3.1). Это - прямая, отсекающая на осях отрезки, равные z. Прямая делит плоскость хОу на две части; правее и выше ее 
; левее и ниже
Область D в данном случае - левая нижняя часть плоскости хОу, заштрихованная на рис. 6.3.1. Согласно формуле (6.3.2) имеем:
Это - общая формула для плотности распределения суммы двух случайных величин.
Из соображений симметричности задачи относительно X и Y можно написать другой вариант той же формулы:
Требуется произвести композицию этих законов, т. е. найти закон распределения величины: .
Применим общую формулу для композиции законов распределения:
Подставляя эти выражения в уже встречавшуюся нам формулу
а это есть не что иное, как нормальный закон с центром рассеивания
К тому же выводу можно прийти значительно проще с помощью следующих качественных рассуждений.
Не раскрывая скобок и не производя преобразований в подынтегральной функции (6.3.3), сразу приходим к выводу, что показатель степени есть квадратный трехчлен относительно х вида
где в коэффициент А величина z не входит совсем, в коэффициент В входит в первой степени, а в коэффициент С - в квадрате. Имея это в виду и применяя формулу(6.3.4), приходим к заключению, что g(z) есть показательная функция, показатель степени которой - квадратный трехчлен относительно z, а плотность аспределения; такого вида соответствует нормальному закону. Таким образом, мы; приходим к чисто качественному выводу: закон распределения величины z должен быть нормальным. Чтобы найти параметры этого закона - и 
- воспользуемся теоремой сложения математических ожиданий и теоремой сложения дисперсий.
По теореме сложения математических ожиданий 
. По теореме сложения дисперсий 
или 
откуда следует формула (6.3.7).
Переходя от среднеквадратических отклонений к пропорциональным им вероятным отклонениям, получим: 
.
Таким образом, мы пришли к следующему правилу: при композиции нормальных законов получается снова нормальный закон, причем математические ожидания и дисперсии (или квадраты вероятных отклонений) суммируются.
Правило композиции нормальных законов может быть обобщено на случай произвольного числа независимых случайных величин.
Если имеется n независимых случайных величин: подчиненных нормальным законам с центрами рассеивания и среднеквадратическими отклонениями ,то величина также подчинена нормальному закону с параметрами
Если система случайных величин (X, Y) распределена по нормальному закону, но величины X, Y зависимы, то нетрудно доказать, так же как раньше, исходя из общей формулы (6.3.1), что закон распределения величины есть тоже нормальный закон. Центры рассеивания по-прежнему складываются алгебраически, но для среднеквадратических отклонений правило становится более сложным: 
, где, r - коэффициент корреляции величин X и Y.
При сложении нескольких зависимых случайных величин, подчиненных в своей совокупности нормальному закону, закон распределения суммы также оказывается нормальным с параметрами
где - коэффициент корреляции величин X i , X j , а суммирование распространяется на все различные попарные комбинации величин .
Мы убедились в весьма важном свойстве нормального закона: при композиции нормальных законов получается снова нормальный закон. Это - так называемое «свойство устойчивости». Закон распределения называется устойчивым, если при композиции двух законов этого типа получается снова закон того же типа. Выше мы показали, что нормальный закон является устойчивым. Свойством устойчивости обладают весьма немногие законы распределения. Закон равномерной плотности неустойчив: при композиции двух законов равномерной плотности на участках от 0 до 1 мы получили закон Симпсона.
Устойчивость нормального закона - одно из существенных условий его широкого распространения на практике. Однако свойством устойчивости, кроме нормального, обладают и некоторые другие законы распределения. Особенностью нормального закона является то, что при композиции достаточно большого числа практически произвольных законов распределения суммарный закон оказывается сколь угодно близок к нормальному вне зависимости от того, каковы были законы распределения слагаемых. Это можно проиллюстрировать, например, составляя композицию трех законов равномерной плотности на участках от 0 до 1. Получающийся при этом закон распределения g(z) изображен на рис. 6.3.1. Как видно из чертежа, график функции g(z) весьма напоминает график нормального закона.
Совместной функцией распределения случайных величин, назовем функцию, зависящую от n вещественных переменных, такую, что Предложение 4.1 (Без доказательства) . Перечислим некоторые свойства функций распределения нескольких случайных величин: Монотонность по каждой переменной, например,
Пределы на ``минус бесконечности"": если в совместной функции распределения зафиксировать все переменные, кроме одной, а оставшуюся переменную устремить к, то предел равен нулю. Например, для фиксированных Пределы на ``плюс бесконечности"".Если все переменные устремить к,в пределе получится единицаЕсли зафиксируем все переменные, кроме одной, которую устремим к, получим функцию распределения меньшего набора случайных величин. Например,
Линии регрессии, корелляции
Если две случайные величины Х и Y имеют в отношении друг друга линейные функции регрессии, то говорят, что величины Х и Y связаны линейной корреляционной зависимостью. Теорема . Если двумерная случайная величина (X, Y) распределена нормально, то Х и Y связаны линейной корреляционной зависимостью.
«Хи-квадрат» - распределение с f степенями свободы, распределение вероятностей суммы квадратов c^2 = X1^2+...+Xf^2, независимых случайных величин X1,..., Xf, подчиняющихся нормальному распределению с нулевым математическим ожиданием и единичной дисперсией. Функция «Х.-к.» р. выражается интегралом
Первые три момента (математическое ожидание дисперсия и третий центральный момент) суммы c2 равны соответственно f, 2f, 8f. Сумма двух независимых случайных величин c1^2 и c2^2, с f^1 и f^2 степенями свободы подчиняется «Х.-к.» р. с f^1 + f^2 степенями свободы. Примерами «Х.-к.» р. могут служить распределения квадратов случайных величин, подчиняющихся Рэлея распределению и Максвелла распределению. В терминах «Х.-к.» р. с чётным числом степеней свободы выражается Пуассона распределение: Если количество слагаемых f суммы c2 неограниченно увеличивается, то согласно центральной предельной теореме распределение нормированного отношения сходится к стандартному нормальному распределению: где
Следствием этого факта является другое предельное соотношение, удобное для вычисления Ff (x) при больших значениях f:
Распределение Стьюдента
Это распределение получило свое название от псевдонима Student, которым английский ученый Госсет подписывал свои работы по статистике. Пусть -- независимые стандартные нормальные случайные величины. Распределением Стьюдента с степенями свободы называется распределениеследующей случайной величины: (46) Если вспомнить введенную формулой (44) случайную величину, то можно сказать, что отношение имеет распределение Стьюдента. Плотность этого распределения представляет собой симметричную функцию, задаваемую формулой По форме график функции напоминает график плотности стандартного нормального закона, но с более медленным убыванием ``хвостов"". При последовательность функций сходится к функции, которая есть плотность распределения. Чтобы понять, почему этот факт имеет место, следует обратить внимание на то, что по закону больших чисел знаменатель выражения (46) при стремится к
