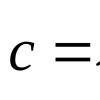Если классическая теория вероятностей изучала, в основном, события и вероятность их появления (наступления), то современная теория вероятностей изучает случайные явления и их закономерности с помощью случайных величин. Понятие случайной величины, таким образом, является основополагающим в теории вероятностей. Ещё ранее проводились события, состоящие в появлении того или иного числа. Например, при бросании игральной кости могли появиться числа 1, 2, 3, 4, 5, 6. Наперёд определить число появившихся очков невозможно, поскольку оно зависит от многих случайных причин, которые полностью не могут быть учтены. В этом смысле число очков есть величина случайная, а числа 1, 2, 3, 4, 5 и 6 есть возможные значения этой величины.

Случайной величиной называется величина, которая в результате опыта принимает то или иное (причём, одно и только одно) возможное числовое значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Случайны величины принято, обычно, обозначать прописными буквами , а их возможное значения - соответствующими строчными буквамиНапример, если случайная величинаимеет три возможных значения, то они, соответственно, обозначаются так:. Для удобства будем писать:.

ПРИМЕР 1 . Число родившихся мальчиков среди ста новорожденных есть величина случайная, которая имеет следующие возможные значения: 0, 1, 2, ..., 100.

ПРИМЕР 2 . Расстояние, которое пролетит снаряд при выстреле из орудия, есть также величина случайная. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т. п.), которые не могут быть полностью учтены. Возможные значения этой величины, очевидно, принадлежат некоторому промежутку (интервалу) .

Заметим, что с каждым случайным событием можно связать какую-либо случайную величину, принимающую значения из R. Например, опыт - выстрел по мишени; событие - попадание в мишень; случайная величина - число попаданий в мишень.

Вернёмся к примерам, приведённым выше. В первом из них случайная величина могла принять одно из следующих возможных значений: 0, 1, 2,..., 100. Эти значения отделены одно от другого промежутками, в которых нет возможных значений. Таким образом, в этом примере случайная величина принимает отдельные, изолированные, возможные значения.

Во втором примере случайная величина могла принять любое из значений промежутка . Здесь нельзя отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины.

Уже из сказанного можно заключить о целесообразности различать случайные величины, принимающие лишь отдельные, изолированные значения и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток.

Дискретной ( прерывной ) случайной величиной называется такая случайная величина, которая принимает конечное или счётное множество 1 различных значений. Другими словами - это такая случайная величина, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.

Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка действительной числовой оси.

Очевидно, во-первых, число возможных значений непрерывной случайной величины – бесконечно. Во-вторых, дискретная случайная величина является частным случаем непрерывной случайной величины.

Закон распределения вероятностей

I . Закон распределения вероятностей дискретной случайной величины

На первый взгляд может показаться, что для задания дискретной случайной величины достаточно перечислить все её возможные значения. В действительности это не так: различные случайные величины иногда могут иметь одинаковые перечни возможных значений, а соответствующие вероятности этих значений – различные. Поэтому для полной характеристики мало знать значения случайной величины, нужно ещё знать, как часто эти значения встречаются в опыте при его повторении, т.е. нужно ещё указать вероятности их появления.

Рассмотрим случайную величину . Появление каждого их возможных значенийсвидетельствует о том, что произошло соответственно одно из событий, которые образуют полную группу 2 . Допустим, что вероятности этих событий известны:

, . . . , ,

Тогда: соответствие, устанавливающее связь между возможными значениями случайной величины и их вероятностями, называется законом распределения вероятностей случайной величины , или просто – законом распределения случайной величины.

Закон распределения вероятностей данной случайной величины можно задать таблично (ряд распределения), аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая - их вероятности, т.е.

В целях наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки , а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения. При этом, сумма ординатпостроенного многоугольника равна единице.

Аналитически закон распределения дискретной случайной величины можно записать, например, используя формулу Бернулли для схемы повторения независимых опытов. Так, если обозначить случайную величину, которой является число бракованных деталей в выборке, через , то возможные её значениябудут 0, 1, 2, . . . ,. Тогда, очевидно, формула Бернулли будет устанавливать зависимость между значениямии вероятностью() их появления, где

,

что о определяет закон распределения данной случайной величины.

II . Закон распределения вероятностей непрерывной случайной величины

Вспомним, что дискретная случайная величина задаётся перечнем всех её возможных значений и их вероятностей. Такой способ задания не является общим: он не применим, например, для непрерывных случайных величин.

Действительно, рассмотрим случайную величину , возможные значения которой сплошь заполняют интервал. Можно ли составить перечень всех возможных значений? Очевидно, что этого сделать нельзя. Этот пример указывает на целесообразность дать общий способ задания любых типов случайных величин (как уже отмечалось, дискретная случайная величина является частным случаем непрерывной случайной величины). С этой целью вводятинтегральную функцию распределения.

Пусть – переменная, принимающая произвольные действительные значения (на оси:) . Рассмотрим событие, состоящее в том, что случайная величинапримет значение меньшее. Тогда, вероятностьсобытиязависит от, т.е. является функцией от. Эту функцию принято обозначать черези называть функцией распределения случайной величины или, ещё – интегральной функцией распределения. Другими словами:

интегральной функцией распределения называют функцию , определяющую для каждого значенияR вероятность того, что случайная величина примет значение, меньшее, т.е.

.

Геометрически это равенство можно истолковывать так: есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки.

Свойства интегральной функции :

Доказательство этого свойства вытекает из определения интегральной функции как вероятности: вероятность всегда есть неотрицательное число, не превышающее единицы.

Действительно, пусть – событие, состоящее в том, что случайная величинапримет значение меньшее; аналогично,
– событие, состоящее в том, что случайная величинапримет значение меньшее. Другими словами:

Следовательно, если , то . Значит (объяснить - почему?)или, что то же самое:

Что и требовалось показать.

Это свойство вполне очевидно. Так, если - достоверное событие, а– невозможное событие, то

Рассмотрим следующие события: . Видим, что– т.е. событияинесовместны. Тогда

Но ,В результате, можем записать:, что и требовалось показать.

Мы будем в основном изучать такие непрерывные случайные величины, функции распределения которых непрерывны.

График функция распределения дискретной случайной величины представляет собой ступенчатую ломаную линию (см. рис.). Величина скачка в точках разрыва равна вероятности значения случайной величины в этой точке. Зная ряд распределения случайной величины, можно построить график её функции распределения:

.

Для непрерывной случайной величины более наглядной является не интегральная, а дифференциальная функция распределения или, так называемая, плотность распределения случайной величины.

Случайная величина как фундаментальное понятие теории вероятности имеет большое значение в ее приложениях. Это понятие является абстрактным выражением случайного события. Более того, оперировать со случайными величинами иногда более удобно, чем со случайными событиями.

Случайной называется величина, которая в результате опыта может принять то или иное (но только одно) значение (до опыта неизвестно, какое именно).

События принято обозначать большими буквами латинского алфавита, вероятность буквой Р, например, Р(А). Реализации события (случайные величины) обозначаются малыми буквами: a 1 , a 2 , …, a n .

Поскольку в теории вероятностей и математической статистике рассматриваются массовые явления, то случайная величина, как правило, характеризуется возможными значениями и их вероятностями.

Среди встречающихся в практике случайных величин можно выделить дискретные и непрерывные.

Дискретными случайными величинами называются такие, которые принимают только отделенные друг от друга значения и могут быть заранее перечислены. Например, количество автомобилей на заданном километровом участке дороги в конкретный момент времени; число бракованных узлов деталей автомобиля в партии из n штук.

Для дискретных случайных величин характерно, что они принимают отдельные, изолированные значения, которые можно заранее перечислить. Например, количество автомобилей на заданном участке дороги может принимать только целочисленные значения 0, 1,2, ..., п и зависит от времени суток и интенсивности движения.

Существуют случайные величины другого типа, которые чаще встречаются и имеют большое практическое значение.

Непрерывной случайной величиной называется такая, возможные значения которой непрерывно заполняют некоторый промежуток (интервал числовой оси). Интервал числовой оси может быть конечным или бесконечным. Примерами непрерывных случайных величин являются время безотказной работы автомобиля в заданных дорожных условиях, скорость движения автомобиля на заданной дороге, ошибка измерения.

В отличие от дискретных возможные значения непрерывных случайных величин нельзя заранее перечислить, так как они непрерывно заполняют некоторый промежуток.

Случайные величины обозначаются обычно большими буквами латинского алфавита - X, Y, Z, Т, а их возможные значения соответствующими малыми x i , y i , z i , t i , где i = 1, 2, .... п.

Рассмотрим дискретную случайную величину X с возможными значениями x 1 , x 2 , …, x n . В результате проведения многократных опытов величина Т может принять каждое из значений x i , т. е.:

X = x 1 ; X = x 2 ; …; X = x n .

Обозначим вероятности этих событий буквой р с соответствующими индексами:

P(X = x 1)= p 1 ; P(X = x 2)= p 2 ; …; P(X = x n)= p n .

Исходя из того, что события x i образуют полную группу несовместимых событий, т. е. никаких других событий произойти не может, сумма вероятностей всех возможных значений случайной величины Т равна единице.

Эта суммарная вероятность каким-то образом распределена между отдельными значениями случайной величины

Дискретную случайную величину можно полностью описать с вероятностной точки зрения, если точно указать вероятность каждого события, т. е. задать это распределение. Этим будет установлен закон распределения случайной величины.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями . Зная его, можно до опыта судить о том, какие значения случайной величины будут появляться чаще и какие реже. Способы или формы представления закона распределения случайной величины различны.

Простейшей формой задания закона распределения дискретной случайной величины Т является ряд распределения или таблица, в которой перечислены возможные значения этой величины и соответствующие им вероятности.

Случайная величина - это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.

Формальное математическое определение следующее: пусть - вероятностное пространство, тогда случайной величиной называется функция , измеримая относительно и борелевской σ-алгебры на . Вероятностное поведение отдельной (независимо от других) случайной величины полностью описывается её распределением.

Определение [править]

Пространство элементарных событий [править]

Пространство элементарных событий в случае бросания игральной кости

Если бросается игральная кость, то в результате верхней гранью может оказаться одна из шести граней с количеством точек от одной до шести. Выпадение какой-либо грани в данном случае в теории вероятностей называется элементарным событием , то есть

Множество всех граней образует пространство элементарных событий , подмножества которого называются случайными событиями . В случае однократного подбрасывания игровой кости примерами событий являются

Алгебра событий [править]

Множество случайных событий образует алгебру событий , если выполняются следующие условия:

Если вместо третьего условия удовлетворяет другому условию: объединение счётного подсемейства из также принадлежит , то множество случайных событий образует σ-алгебру событий.

Алгебра событий является частным случаем σ-алгебры множеств.

Самая маленькая среди всех возможных -алгебр, элементами которой являются все интервалы на вещественной прямой, называется борелевской σ-алгеброй на множестве вещественных чисел .

Вероятность [править]

Если каждому элементарному событию поставить в соответствие число , для которого выполняется условие:

то считается, что заданы вероятности элементарных событий . Вероятность события, как счётного подмножества пространства элементарных событий, определяется как сумма вероятностей тех элементарных событий, которые принадлежат этому событию. Требование счётности важно, так как, иначе сумма будет не определена.

Рассмотрим пример определения вероятности различных случайных событий. Например, если событие является пустым множеством, то его вероятность равна нулю :

Если событием является пространство элементарных событий, то его вероятность равна единице:

Вероятность события (подмножества пространства элементарных событий) равна сумме вероятностей тех элементарных событий, которые включает в себя рассматриваемое событие.

Определение случайной величины [править]

Случайной величиной называется функция , измеримая относительно и борелевской σ-алгебры на .

Случайную величину можно определить и другим эквивалентным способом . Функция называется случайной величиной, если для любых вещественных чисел и множество событий , таких что , принадлежит .

Примеры [править]

равно среднему арифметическому всех принимаемых значений.

.

,

то есть математическое ожидание не определено.

Классификация [править]

Случайные величины могут принимать дискретные, непрерывные и дискретно-непрерывные значения. Соответственно случайные величины классифицируют на дискретные, непрерывные и дискретно-непрерывные (смешанные).

На схеме испытаний может быть определена как отдельная случайная величина (одномерная/скалярная), так и целая система одномерных взаимосвязанных случайных величин (многомерная/векторная).

• Пример смешанной случайной величины - время ожидания при переходе через автомобильную дорогу в городе на нерегулируемом перекрёстке.
• В бесконечных схемах (дискретных или непрерывных) уже изначально элементарные исходы удобно описывать количественно. Например, номера градаций типов несчастных случаев при анализе ДТП; время безотказной работы прибора при контроле качества и т. п.
• Числовые значения, описывающие результаты опытов, могут характеризовать не обязательно отдельные элементарные исходы в схеме испытаний, но и соответствовать каким-то более сложным событиям.

С одной стороны, с одной схемой испытаний и с отдельными событиями в ней одновременно может быть связано сразу несколько числовых величин, которые требуется анализировать совместно.

• Например, координаты (абсцисса, ордината) какого-то разрыва снаряда при стрельбе по наземной цели; метрические размеры (длина, ширина и т. д.) детали при контроле качества; результаты медобследования (температура, давление, пульс и пр.) при диагностике больного; данные переписи населения (по возрасту, полу, достатку и пр.).

Поскольку значения числовых характеристик схем испытания соответствуют в схеме некоторым случайным событиям (с их определёнными вероятностями), то и сами эти значения являются случайными (с теми же вероятностями). Поэтому такие числовые характеристики и принято называть случайными величинами. При этом расклад вероятностей по значениям случайной величины называется законом распределения случайной величины.

Методы описания [править]

Частично задать случайную величину, описав этим все её вероятностные свойства как отдельной случайной величины, можно с помощью функции распределения, плотности вероятности и характеристической функции, определяя вероятности возможных её значений. Функция распределения F(x) является вероятностью того, что значения случайной величины меньше вещественного числа x. Из этого определения следует, что вероятность попадания значения случайной величины в интервал

Случайная величина, вообще говоря, может принимать значения в любом измеримом пространстве. Тогда её чаще называют случайным вектором или случайным элементом. Например,

См. также [править]

• Случайный процесс
• Функция распределения
• Математическое ожидание

Примечания [править]

1. 1 2 Чернова Н. И. Глава 1. § 2. Элементарная теория вероятностей // Теория вероятностей. - Учебное пособие. - Новосибирск: Новосибирский гос. ун-т, 2007. - 160 с.
2. Чернова Н. И. Глава 3. § 1. Алгебра и сигма-алгебра событий // Теория вероятностей. - Учебное пособие. - Новосибирск: Новосибирский гос. ун-т, 2007. - 160 с.
3. Чернова Н. И. ГЛАВА 1 § 2. Элементарная теория вероятностей // Теория вероятностей. - Учебное пособие. - Новосибирск: Новосибирский гос. ун-т, 2007. - 160 с.
4. 1 2 Чернова Н. И. Глава 6. Случайные величины и их распределения § 1. Случайные величины // Теория вероятностей. - Учебное пособие. - Новосибирск: Новосибирский гос. ун-т, 2007. - 160 с.

Литература [править]

• Гнеденко Б. В. Курс теории вероятности. - 8-е изд. доп. и испр. - М.: Едиториал УРСС, 2005. - 448 с.
• Математический энциклопедический словарь / Гл. ред. Прохоров Ю. В.. - 2-е изд. - М.: «Советская энциклопедия», 1998. - 847 с.
• Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. - Учебное пособие для ВУЗов. - М.: Радио и связь, 1991. - 608 с. - ISBN 5-256-00789-0
• Чернова Н. И. Теория вероятностей. - Учебное пособие. - Новосибирск: Новосибирский гос. ун-т, 2007. - 160 с.

Одним из важнейших основных понятий теории вероятностей является понятие о случайной величине.

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.

Примеры случайных величин:

1) число попаданий при трех выстрелах;

2) число вызовов, поступавших на телефонную станцию за сутки;

3) частота попадания при 10 выстрелах.

Во всех трех приведенных примерах случайные величины могут принимать отдельные, изолированные значения, которые можно заранее перечислить.

Так, в примере 1) эти значения:

в примере 2):

в примере 3)

0; 0,1; 0,2; …; 1,0.

Такие случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить, называются прерывными или дискретными случайными величинами.

Существуют случайные величины другого типа, например:

1) абсцисса точки попадания при выстреле;

2) ошибка взвешивания тела на аналитических весах;

3) скорость летательного аппарата в момент выхода на заданную высоту;

4) вес наугад взятого зерна пшеницы.

Возможные значения таких случайных величин не отделены друг от друга; они непрерывно заполняют некоторый промежуток, который иногда имеет резко выраженные границы, а чаще – границы неопределенные, расплывчатые.

Такие случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток, называются непрерывными случайными величинами.

Понятие случайной величины играет весьма важную роль в теории вероятностей. Если «классическая» теория вероятностей оперировала по преимуществу с событиями, то современная теория вероятностей предпочитает, где только возможно, оперировать со случайными величинами.

Приведем примеры типичных для теории вероятностей приемов перехода от событий к случайным величинам.

Производится опыт, в результате которого может появиться или не появиться некоторое событие. Вместо события можно рассмотреть случайную величину , которая равна 1, если событие происходит, и равна 0, если событие не происходит. Случайная величина, очевидно, является прерывной; она имеет два возможных значения: 0 и 1. Эта случайная величина называется характеристической случайной величиной события . На практике часто вместо событий оказывается удобнее оперировать их характеристическими случайными величинами. Например, если производится ряд опытов, в каждом из которых возможно появление события , то общее число появлений события равно сумме характеристических случайных величин события во всех опытах. При решении многих практических задач пользование таким приемом оказывается очень удобным.

С другой стороны, очень часто для вычисления вероятности события оказывается удобно связать это событие с какой-то непрерывной случайной величиной (или системой непрерывных величин).

Пусть, например, измеряются координаты какого-то объекта О для того, чтобы построить точку М, изображающую этот объект на панораме (развертке) местности. Нас интересует событие , состоящее в том, что ошибка R в положении точки М не превзойдет заданного значения (рис. 2.4.1). Обозначим случайные ошибки в измерении координат объекта. Очевидно, событие равносильно попаданию случайной точки М с координатами в пределы круга радиуса с центром в точке О. Другими словами, для выполнения события случайные величины и должны удовлетворять неравенству

Вероятность события есть не что иное, как вероятность выполнения неравенства (2.4.1). Эта вероятность может быть определена, если известны свойства случайных величин .

Такая органическая связь между событиями и случайными величинами весьма характерна для современной теории вероятностей, которая, где только возможно, переходит от «схемы событий» к «схеме случайных величин». Последняя схема сравнительно с первой представляет собой гораздо более гибкий и универсальный аппарат для решения задач, относящихся к случайным явлениям.

Расширением понятия случайных событий, состоящих в появлении некоторых числовых значений в результате эксперимента, является случайная величина Х.

Определение. Случайной называют величину, принимающую в результате эксперимента одно только значение из некоторой их совокупности и неизвестное заранее, какое именно.

Случайная величина , к примеру, представляет собой обоснованную модель описания геологических данных, учитывающую влияние различных факторов на физическое поле .

Как и результат отдельного эксперимента, точное значение случайной величины предсказать нельзя, можно лишь установить ее статистические закономерности, т.е. определить вероятности значений случайной величины. Например, измерения физических свойств горных пород являются наблюдениями соответствующих случайных величин.

Среди случайных величин, с которыми приходится встречаться геологу, можно выделить два основных типа: величины дискретные и величины непрерывные .

Определение. Дискретной случайной величиной называется такая, которая может принимать конечное или бесконечное счетное множество значений.

В качестве типичных примеров дискретной случайной величины могут выступать все результаты полевых работ , все результаты экспериментов, привезенные c поля образцы и пр.

Всевозможные значений случайной величины образуют полную группу событий, т.е. , где - конечное или бесконечное. Поэтому можно говорить, что случайная величина обобщает понятие случайного события.

Пусть в результате исследований был получен следующий ряд данных по количественному составу некоторой породы: 4; 3; 1; 2; 5; 4; 2; 2; 3; 1; 5; 4; 3; 5; 5; 2; 5; 5; 6; 1. Всего было проведено 20 испытаний. Для того, чтобы с данными было удобно работать, их преобразовали: расположили полученные значения по возрастанию и подсчитали количество появления каждого из значений. В результате получили (Таблица 7.1):

Определение . Распределение данных по возрастанию называется ранжированием .

Определение . Наблюдаемое значение некоторого признака случайной величины называется вариантом.

Определение . Ряд, составленный из вариант, называется вариационным рядом .

Определение . Изменение некоторого признака случайной величины называется варьированным .

Определение . Число, показывающее сколько раз варьируется данная варианта, называется частотой и обозначается .

Определение. Вероятность появления данной варианты равно отношению частоты к общей сумме вариационного ряда

(1)

С учетом введенных определений перепишем таблицу 7.1 .

Таблица 7.2. Ранжированный ряд

Вариант	1	2	3	4	5	6
Частота	3	4	3	3	6	1
Вероятность	3/20	4/20	3/20	3/20	6/20	1/20

При статистическом анализе экспериментальных данных главным образом используется дискретные величины. В таблице 7.3 приведены основные числовые характеристики этих величин, имеющих важное практическое значение при обработке экспериментальных данных.

Таблица 7.3. Числовые характеристики случайных величин

N п/п	Характеристика (параметр) случайной величины и ее обозначение	Формула для нахождения характеристики случайной величины	Примечание
1	Математическое ожидание	(2)	Характеризует положение случайной величины на числовой оси
2	Среднее значение	(3)	Если случайная величина независимая, то
3	Мода	Это такое значение , для которого наиболь-шее	Равна наиболее часто встречающемуся значению . Если таких значений в вариационном ряду несколько, то не определяется.
4	Медиана	Если четное, то Если нечетное, то	Это такое значение, которое находится в центре ранжированного ряда.
5	Дисперсия		Характеризует действительное рассеяние случайной величины вокруг среднего значения.
7	Коэффициент вариации	(6)	Наряду с дисперсией характеризует изменчивость случайной величины
8	Центрированное нормированное уклонение